서론
마땅히 생각나는 이름이 없어서 아무렇게나 지었습니다.
먼저, 세그먼트 트리를 모르신다면 여기서 보고 오시는 것을 추천합니다.
BOJ북이 참 성능이 좋습니다.
소개
쓸 수 있는 문제
어떤 수열 $A_n$이 주어졌을 때,
- $A_i$부터 $A_j$까지 더하는 쿼리,
- $A_i$를 출력하는 쿼리
와 같이 구간을 업데이트 하고 하나의 값을 요구하는 문제에서 사용 가능합니다.
위와 같은 문제의 전형적인 예제로서 수열과 쿼리 21이 있습니다.
쓸 수 없는 문제
점 출력이 아니라 구간이라면 이 테크닉은 사용할 수 없고, 느리게 갱신되는 세그먼트 트리를 사용해야 합니다.
구간 합 구하기 2와 같은 문제가 여기에 해당합니다.
또 쿼리의 순서가 상관있는 경우에는 사용할 수 없습니다.
벽과 같은 문제가 여기에 해당합니다.
아이디어
아이디어는 그렇게 어렵지 않습니다.
lazyprop은 구간에 더할 값을 저장해 뒀다가 나중에 쿼리가 들어올 때 트리를 갱신하는 방식으로 시간복잡도를 줄였습니다. 이 방식도 비슷한데요, 구간에 더할 값을 저장해두고, 쿼리가 들어오면 해당 노드까지 가는 경로의 값을 모두 더합니다.
세그먼트 트리의 각각의 노드가 자신이 담당하는 범위에 더할 값을 저장해 놓게 되는 것입니다.
그림과 함께 한번 봅시다.
예를 들어, $A_n = [ 1, 2, 3, 4, 5, 6, 7, 8 ]$ 으로 주어졌다고 합시다.

세그먼트 트리는 위와 같이 초기화됩니다.
세그먼트 트리의 노드에 적혀있는 값들은 위에서부터
- 노드의 번호
- 노드가 담당하는 범위
- 노드에 저장된 값
을 의미합니다.
이때, 인덱스 0부터 5까지 10을 더하라는 쿼리가 들어왔다고 합시다.
1번 노드부터 시작합니다. 1번 노드가 담당하는 범위는 $[0, 7]$로, $[0, 5]$에 포함되지 않으니 자식 노드로 업데이트를 이어나갑니다.
2번 노드가 담당하는 범위는 $[0, 3]$로, $[0, 5]$에 포함됩니다. 따라서 2번 노드에 10이라는 값을 더해줍니다.
3번 노드가 담당하는 범위는 $[4, 7]$로, $[0, 5]$에 포함되지 않으니 자식 노드로 업데이트를 이어나갑니다.
6번 노드가 담당하는 범위는 $[4, 5]$로, $[0, 5]$에 포함됩니다. 따라서 6번 노드에 10이라는 값을 더해줍니다.
7번 노드가 담당하는 범위는 $[6, 7]$로, $[0, 5]$와 겹치지 않습니다. 따라서 탐색을 종료합니다.
모든 업데이트를 마치고 나면 $A_n$과 트리는 아래와 같이 변합니다.
$A_n = [ 11, 12, 13, 14, 15, 6, 7, 8 ]$
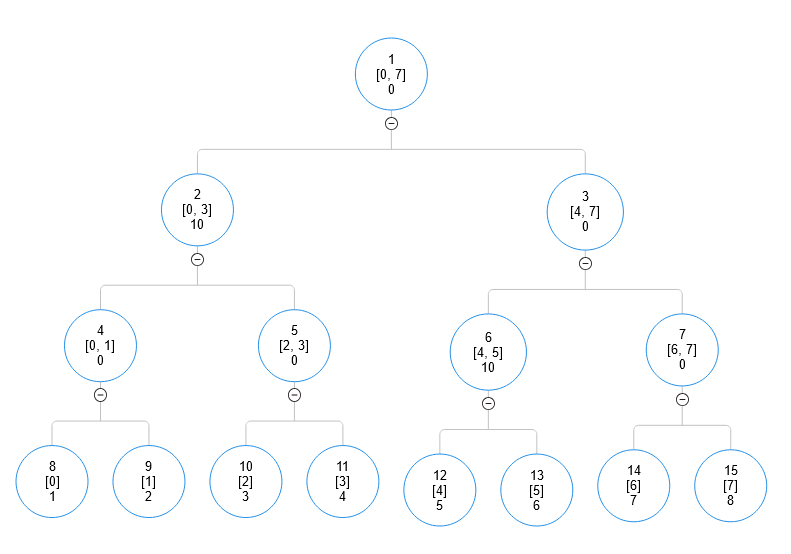
트리를 보면, $[i, i]$범위를 담당하는 리프노드의 값과 그 노드의 부모 노드의 값을 모두 합치면 $A_n$의 값이 나옵니다.
이와 같은 방식으로 lazy배열 없이 없이 구간 업데이트 쿼리를 처리할 수 있습니다.