백준 13976번: 타일 채우기 2 [C++]

작성일 | In
플래티넘 V 플래티넘 V

문제

타일 채우기 2

풀이

$N \equiv 1 \pmod 2$인 경우는 해가 존재하지 않음을 직관적으로 알 수 있습니다.

$N \equiv 0 \pmod 2$인 경우만 살펴봅시다. $N = i$인 경우의 답을 $T_i$라 합시다. 초기값으로 $T_0 = 1$입니다.

점화식

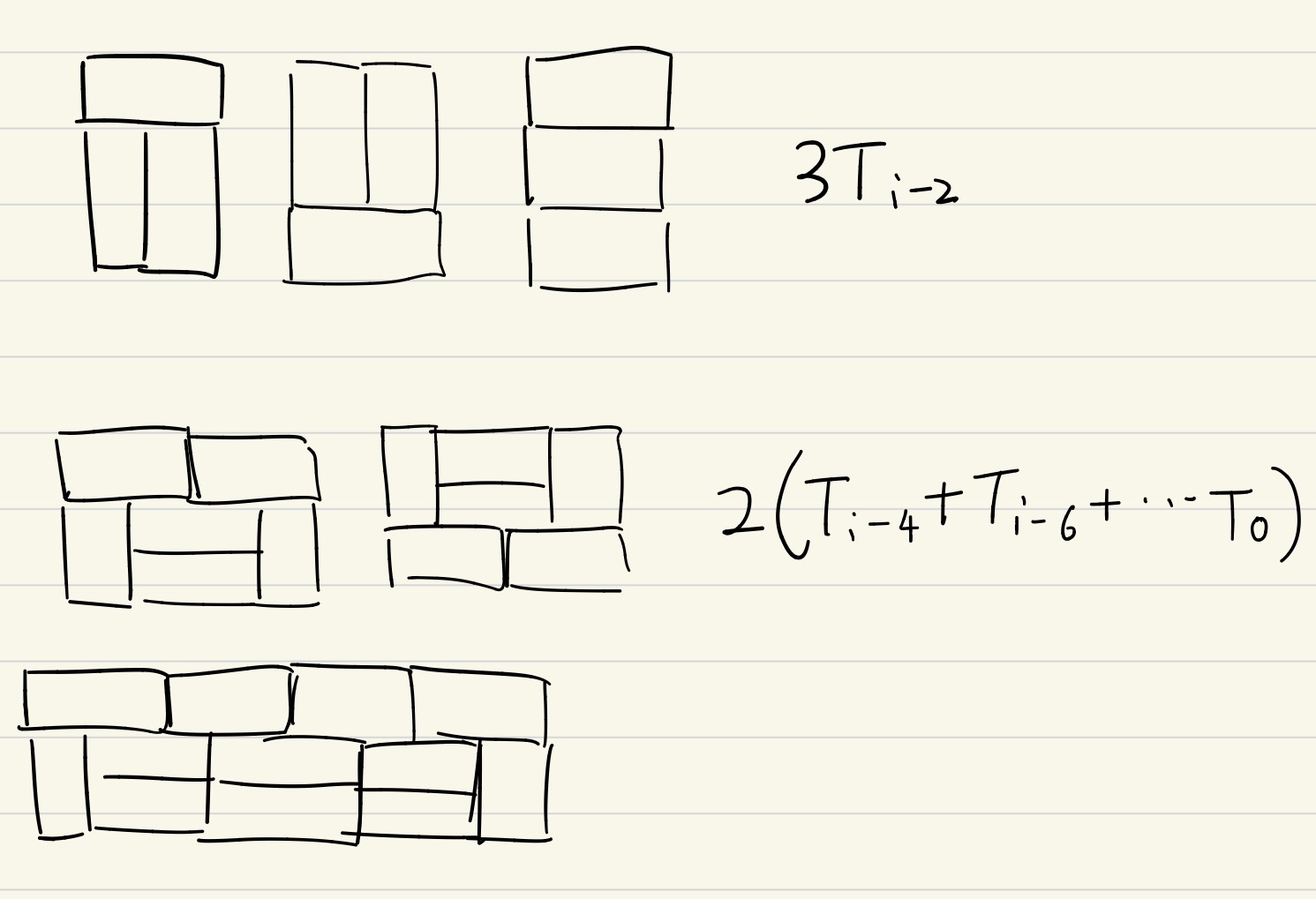
위 사진을 통해 아래와 같은 점화식을 구할 수 있습니다.

\[T_i = 3T_{i - 2} + 2(T_{i - 4} + T_{i - 6} + \dots + T_0)\]

여기서 $i$ 대신 $i + 2$를 대입해 아래와 같은 식을 얻습니다.

\[T_{i + 2} = 3T_i + 2(T_{i - 2} + T_{i - 4} + \dots + T_0)\]

이제 $T_{i + 2}$에서 $T_i$를 빼서 아래의 식을 얻습니다.

\[\begin{align} T_{i + 2} - T_i &= 3T_i - T_{i - 2} \\ T_{i + 2} &= 4T_i - T_{i - 2} \end{align}\]

그렇다면 행렬을 이용해 아래와 같이 나타낼 수 있습니다.

\[\begin{bmatrix} 4 & -1 \\ 1 & 0 \end{bmatrix} \begin{bmatrix} T_i \\ T_{i - 2} \end{bmatrix} = \begin{bmatrix} T_{i + 2} \\ T_i \end{bmatrix}\]

여기서 $T_0 = 1$이고 $T_2 = 3$이므로

\[\begin{bmatrix} 4 & -1 \\ 1 & 0 \end{bmatrix}^{k - 1} \begin{bmatrix} 3 \\ 1 \end{bmatrix} = \begin{bmatrix} T_{2k} \\ T_{2k - 2} \end{bmatrix}\]

이제 분할 정복을 이용한 거듭제곱을 통해 $T_N$을 계산해주면 됩니다.

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
#include <bits/stdc++.h>
#ifndef ONLINE_JUDGE
#define ASSERT(x) assert(x)
#else
#define ASSERT(ignore) ((void)0)
#endif

using namespace std;

using ll = long long;

constexpr int MOD = 1e9 + 7;

template <typename T>
using Matrix = vector<vector<T>>;

template <typename T>
Matrix<T> operator*(const Matrix<T>& m1, const Matrix<T>& m2) {
    Matrix<T> ret(m1.size(), vector<T>(m2[0].size()));

    for (int i = 0; i < (int)m1.size(); i++) {
        for (int j = 0; j < (int)m2[0].size(); j++) {
            for (int k = 0; k < (int)m2.size(); k++) {
                ret[i][j] +=
                    ((m1[i][k] % MOD) * (m2[k][j] % MOD) % MOD + MOD) % MOD;
                ret[i][j] = (ret[i][j] % MOD + MOD) % MOD;
            }
        }
    }

    return ret;
}

Matrix<ll> base = {
    {3},
    {1},
};
Matrix<ll> mul = {
    {4, -1},
    {1, 0},
};

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    ll N;
    cin >> N;

    if (N & 1) {
        print("0");
        return 0;
    }

    N >>= 1;
    N--;
    while (N) {
        if (N & 1)
            base = mul * base;
        mul = mul * mul;
        N >>= 1;
    }

    print("{}", base[0][0]);

    return 0;
}

백준 13976번: 타일 채우기 2 [C++]